ပိုလာရိုက်ဇေးရှင်းသည် အင်တင်နာများ၏ အခြေခံဝိသေသလက္ခဏာများထဲမှ တစ်ခုဖြစ်သည်။ ကျွန်ုပ်တို့သည် ဦးစွာ မျက်နှာပြင်လှိုင်းများ၏ ပိုလာရိုက်ဇေးရှင်းကို နားလည်ရန် လိုအပ်ပါသည်။ ထို့နောက် အင်တင်နာ ပိုလာရိုက်ဇေးရှင်း၏ အဓိကအမျိုးအစားများကို ဆွေးနွေးနိုင်ပါသည်။
linear polarization
ကျွန်ုပ်တို့သည် ပြားချပ်လျှပ်စစ်သံလိုက်လှိုင်း၏ ပိုလာရိုက်ဇေးရှင်းကို နားလည်လာပါမည်။
ပြားချပ်လျှပ်စစ်သံလိုက်လှိုင်း (EM) တွင် ဝိသေသလက္ခဏာများစွာရှိသည်။ ပထမအချက်မှာ ပါဝါသည် တစ်ဖက်သို့ ရွေ့လျားသည် (ထောင့်မှန် ဦးတည်ချက်နှစ်ခုတွင် စက်ကွင်းမပြောင်းလဲပါ)။ ဒုတိယအချက်မှာ လျှပ်စစ်စက်ကွင်းနှင့် သံလိုက်စက်ကွင်းသည် တစ်ခုနှင့်တစ်ခု ထောင့်မှန်ကျပြီး တစ်ခုနှင့်တစ်ခု ထောင့်မှန်ကျသည်။ လျှပ်စစ်နှင့် သံလိုက်စက်ကွင်းများသည် ပြားချပ်လှိုင်းပျံ့နှံ့မှု ဦးတည်ချက်နှင့် ထောင့်မှန်ကျသည်။ ဥပမာအားဖြင့်၊ ညီမျှခြင်း (1) ဖြင့်ပေးထားသော ကြိမ်နှုန်းတစ်ခုတည်းရှိသော လျှပ်စစ်စက်ကွင်း (E စက်ကွင်း) ကို စဉ်းစားပါ။ လျှပ်စစ်သံလိုက်စက်ကွင်းသည် +z ဦးတည်ချက်ဖြင့် ရွေ့လျားနေသည်။ လျှပ်စစ်စက်ကွင်းသည် +x ဦးတည်ချက်ဖြင့် ရွေ့လျားနေသည်။ သံလိုက်စက်ကွင်းသည် +y ဦးတည်ချက်တွင် ရှိသည်။
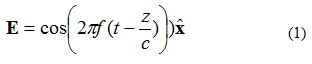
ညီမျှခြင်း (1) တွင်၊ သင်္ကေတကို သတိပြုပါ- . ၎င်းသည် ယူနစ်ဗက်တာ (အလျား၏ ဗက်တာ) တစ်ခုဖြစ်ပြီး လျှပ်စစ်စက်ကွင်းအမှတ်သည် x ဦးတည်ရာတွင် ရှိသည်ဟု ဖော်ပြထားသည်။ မျက်နှာပြင်လှိုင်းကို ပုံ ၁ တွင် သရုပ်ဖော်ထားသည်။
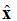
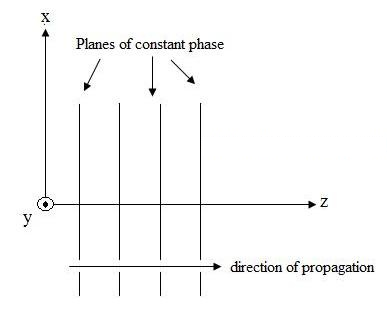
ပုံ ၁။ +z ဦးတည်ချက်ဖြင့် ခရီးသွားနေသော လျှပ်စစ်စက်ကွင်း၏ ဂရပ်ဖစ်ပုံစံဖြင့် ပုံဖော်ပြသထားသည်။
ပိုလာရိုက်ဇေးရှင်းဆိုသည်မှာ လျှပ်စစ်စက်ကွင်း၏ ခြေရာခံခြင်းနှင့် ပျံ့နှံ့ခြင်းပုံသဏ္ဍာန် (ကွန်တို) ဖြစ်သည်။ ဥပမာအားဖြင့်၊ မျက်နှာပြင်လှိုင်း လျှပ်စစ်စက်ကွင်းညီမျှခြင်း (1) ကို ထည့်သွင်းစဉ်းစားပါ။ လျှပ်စစ်စက်ကွင်းသည် အချိန်၏ လုပ်ဆောင်ချက်အနေဖြင့် (X,Y,Z) = (0,0,0) ဖြစ်သည့် နေရာကို ကျွန်ုပ်တို့ လေ့လာကြည့်ရှုပါမည်။ ဤစက်ကွင်း၏ လွှဲအပ်မှုကို ပုံ ၂ တွင် အချိန်ကာလများစွာတွင် ပုံဖော်ထားသည်။ စက်ကွင်းသည် ကြိမ်နှုန်း "F" တွင် တုန်ခါနေသည်။
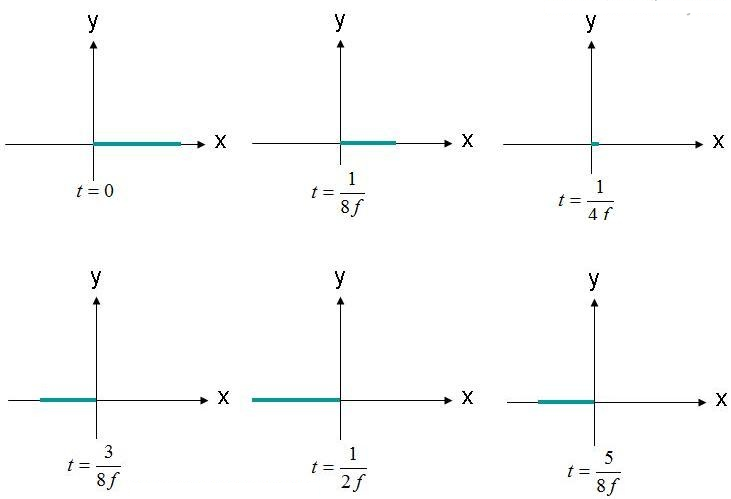
ပုံ ၂။ လျှပ်စစ်စက်ကွင်း (X, Y, Z) = (0,0,0) ကို အချိန်အမျိုးမျိုးတွင် ကြည့်ပါ။
လျှပ်စစ်စက်ကွင်းကို မူလအစတွင် amplitude ဖြင့် ရှေ့တိုးနောက်ငင် ယိမ်းနွဲ့နေသည်ကို တွေ့ရှိရသည်။ လျှပ်စစ်စက်ကွင်းသည် ညွှန်ပြထားသော x-ဝင်ရိုးတစ်လျှောက်တွင် အမြဲရှိသည်။ လျှပ်စစ်စက်ကွင်းကို မျဉ်းတစ်ကြောင်းတည်းတစ်လျှောက် ထိန်းသိမ်းထားသောကြောင့် ဤစက်ကွင်းကို linearly polarized ဖြစ်သည်ဟု ဆိုနိုင်သည်။ ထို့အပြင် X-ဝင်ရိုးသည် မြေပြင်နှင့်အပြိုင်ဖြစ်ပါက ဤစက်ကွင်းကို horizontally polarized ဟုလည်း ခေါ်သည်။ စက်ကွင်းသည် Y-ဝင်ရိုးတစ်လျှောက်တွင် တည်ရှိပါက လှိုင်းကို vertical polarized ဖြစ်သည်ဟု ဆိုနိုင်သည်။
လိုင်းနရီပိုလာရိုက်လှိုင်းများကို အလျားလိုက် သို့မဟုတ် ဒေါင်လိုက်ဝင်ရိုးတစ်လျှောက် ဦးတည်ရန် မလိုအပ်ပါ။ ဥပမာအားဖြင့်၊ ပုံ ၃ တွင်ပြထားသည့်အတိုင်း မျဉ်းတစ်ကြောင်းတစ်လျှောက် ကန့်သတ်ချက်ရှိသော လျှပ်စစ်စက်ကွင်းလှိုင်းတစ်ခုသည်လည်း လိုင်းနရီပိုလာရိုက်လှိုင်းဖြစ်သည်။
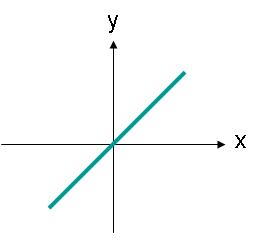
ရုပ်ပုံ ၃။ ထောင့်လမ်းကြောင်းဖြစ်သော မျဉ်းဖြောင့်ပိုလာရိုက်ဇ်လှိုင်း၏ လျှပ်စစ်စက်ကွင်း amplitude။
ပုံ ၃ ရှိ လျှပ်စစ်စက်ကွင်းကို ညီမျှခြင်း (2) ဖြင့် ဖော်ပြနိုင်သည်။ ယခု လျှပ်စစ်စက်ကွင်း၏ x နှင့် y အစိတ်အပိုင်းတစ်ခု ရှိသည်။ အစိတ်အပိုင်းနှစ်ခုလုံးသည် အရွယ်အစားတူညီကြသည်။
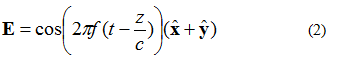
ညီမျှခြင်း (2) နှင့်ပတ်သက်၍ မှတ်သားထားရမည့်အချက်တစ်ခုမှာ ဒုတိယအဆင့်ရှိ xy-component နှင့် electronic fields ဖြစ်သည်။ ဆိုလိုသည်မှာ အစိတ်အပိုင်းနှစ်ခုလုံးသည် အချိန်တိုင်းတွင် တူညီသော amplitude ရှိသည်။
စက်ဝိုင်းပုံ ပိုလာရိုက်ဇေးရှင်း
ယခု မျက်နှာပြင်လှိုင်း၏ လျှပ်စစ်စက်ကွင်းကို ညီမျှခြင်း (3) ဖြင့် ပေးထားသည်ဟု ယူဆပါ-
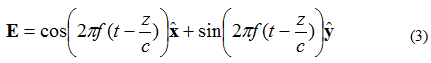
ဤကိစ္စတွင် X- နှင့် Y- ဒြပ်စင်များသည် အဆင့်မှ ၉၀ ဒီဂရီ လွဲနေပါသည်။ အကယ်၍ ယခင်ကကဲ့သို့ စက်ကွင်းကို (X, Y, Z) = (0,0,0) အဖြစ် ပြန်လည်တွေ့ရှိရပါက၊ လျှပ်စစ်စက်ကွင်းနှင့် အချိန်ကွေးသည် အောက်ပါပုံ ၄ တွင် ပြထားသည့်အတိုင်း ပေါ်လာမည်ဖြစ်သည်။
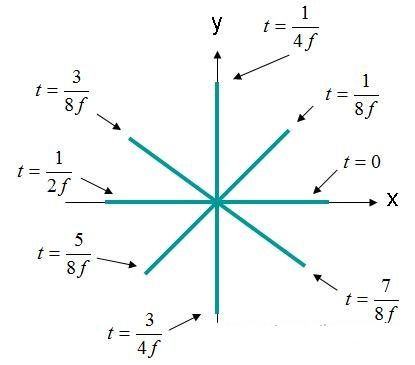
ပုံ ၄။ လျှပ်စစ်စက်ကွင်းအစွမ်းသတ္တိ (X, Y, Z) = (0,0,0) EQ ဒိုမိန်း။ (3)။
ပုံ ၄ ရှိ လျှပ်စစ်စက်ကွင်းသည် စက်ဝိုင်းပုံသဏ္ဍာန်ဖြင့် လည်ပတ်သည်။ ဤစက်ကွင်းအမျိုးအစားကို စက်ဝိုင်းပုံ ပိုလာရိုက်ဇေးရှင်းလှိုင်းအဖြစ် ဖော်ပြထားသည်။ စက်ဝိုင်းပုံ ပိုလာရိုက်ဇေးရှင်းအတွက် အောက်ပါစံနှုန်းများနှင့် ကိုက်ညီရမည်။
- စက်ဝိုင်းပုံ ပိုလာရိုက်ဇေးရှင်းအတွက် စံနှုန်း
- လျှပ်စစ်စက်ကွင်းတွင် ထောင့်မှန် (ထောင့်မှန်) အစိတ်အပိုင်းနှစ်ခု ရှိရမည်။
- လျှပ်စစ်စက်ကွင်း၏ orthogonal အစိတ်အပိုင်းများသည် တူညီသော amplitude ရှိရမည်။
- quadrature အစိတ်အပိုင်းများသည် phase မှ ၉၀ ဒီဂရီ လွဲနေရမည်။
Wave Figure 4 မျက်နှာပြင်ပေါ်တွင် ခရီးသွားနေပါက၊ စက်ကွင်းလည်ပတ်မှုသည် နာရီလက်တံပြောင်းပြန်ဖြစ်ပြီး ညာလက်ဖြင့် စက်ဝိုင်းပုံ polarization (RHCP) ဖြစ်သည်ဟု ဆိုပါသည်။ စက်ကွင်းကို နာရီလက်တံလည်သည့် ဦးတည်ရာအတိုင်း လည်ပတ်ပါက၊ စက်ကွင်းသည် ဘယ်ဘက်လက်ဖြင့် စက်ဝိုင်းပုံ polarization (LHCP) ဖြစ်လိမ့်မည်။
ဘဲဥပုံ ပိုလာရိုက်ဇေးရှင်း
လျှပ်စစ်စက်ကွင်းတွင် ထောင့်မှန်အစိတ်အပိုင်းနှစ်ခု၊ အဆင့်မှ ၉၀ ဒီဂရီ လွဲနေသော်လည်း ပမာဏတူညီပါက၊ စက်ကွင်းသည် elliptical polarized ဖြစ်လိမ့်မည်။ +z ဦးတည်ချက်ဖြင့် ခရီးသွားနေသော မျက်နှာပြင်လှိုင်း၏ လျှပ်စစ်စက်ကွင်းကို ထည့်သွင်းစဉ်းစားပါက၊ Equation (4) ဖြင့်ဖော်ပြထားသည်-
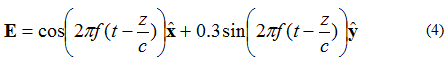
လျှပ်စစ်စက်ကွင်း ဗက်တာ၏ အဖျားက ယူဆမည့် အမှတ်၏ locus ကို ပုံ ၅ တွင် ဖော်ပြထားသည်။
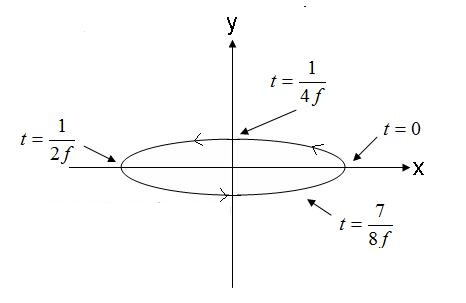
ပုံ ၅။ elliptical polarization wave electric field ကို အချက်ပြပါ။ (4)။
ပုံ ၅ ရှိ စက်ကွင်းသည် နာရီလက်တံပြောင်းပြန် ဦးတည်ရာအတိုင်း ခရီးသွားနေပြီး မျက်နှာပြင်မှ ထွက်ခွာသွားပါက ညာသန်ဘက်သုံး ဘဲဥပုံသဏ္ဍာန် ဖြစ်လိမ့်မည်။ လျှပ်စစ်စက်ကွင်း ဗက်တာသည် ဆန့်ကျင်ဘက် ဦးတည်ရာသို့ လည်ပတ်ပါက စက်ကွင်းသည် ဘယ်ဘက်သန်ဘက်သုံး ဘဲဥပုံသဏ္ဍာန် ပိုလာရိုက် ဖြစ်နေလိမ့်မည်။
ထို့အပြင်၊ elliptical polarization ဆိုသည်မှာ ၎င်း၏ eccentricity ကို ရည်ညွှန်းသည်။ eccentricity နှင့် major နှင့် minor axis များ၏ amplitude အချိုး။ ဥပမာအားဖြင့်၊ equation (4) မှ wave eccentricity သည် 1/0.3 = 3.33 ဖြစ်သည်။ Elliptically polarized waves များကို major axis ၏ ဦးတည်ရာဖြင့် ထပ်မံဖော်ပြပါသည်။ wave equation (4) တွင် x-axis အဓိကအားဖြင့် ပါဝင်သည့် axis တစ်ခုရှိသည်။ major axis သည် မည်သည့် plane angle တွင်မဆို ရှိနိုင်ကြောင်း သတိပြုပါ။ X၊ Y သို့မဟုတ် Z axis နှင့် ကိုက်ညီရန် angle မလိုအပ်ပါ။ နောက်ဆုံးအနေဖြင့်၊ circular နှင့် linear polarization နှစ်မျိုးလုံးသည် elliptical polarization ၏ အထူးကိစ္စရပ်များဖြစ်ကြောင်း မှတ်သားထားရန် အရေးကြီးပါသည်။ 1.0 eccentric elliptically polarized wave သည် circularly polarized wave တစ်ခုဖြစ်သည်။ အဆုံးမဲ့ eccentricity ရှိသော Elliptically polarized waves များ။ Linearly polarized waves များ။
အင်တင်နာ ပိုလာရိုက်ဇေးရှင်း
ယခု ကျွန်ုပ်တို့သည် polarized plane wave electromagnetic fields များအကြောင်း သိရှိပြီးဖြစ်သောကြောင့် antenna ၏ polarization ကို ရိုးရှင်းစွာ သတ်မှတ်ပါသည်။
အင်တင်နာ ပိုလာရိုက်ဇေးရှင်း ဆိုသည်မှာ အင်တင်နာ၏ အဝေးကွင်း အကဲဖြတ်ချက်ဖြစ်ပြီး၊ ရလဒ်အနေဖြင့် ဖြာထွက်နေသော စက်ကွင်း၏ ပိုလာရိုက်ဇေးရှင်းဖြစ်သည်။ ထို့ကြောင့် အင်တင်နာများကို မကြာခဏ "linearly polarized" သို့မဟုတ် "right-handed circularly polarized antennas" အဖြစ် စာရင်းသွင်းလေ့ရှိသည်။
ဒီရိုးရှင်းတဲ့ အယူအဆဟာ အင်တင်နာ ဆက်သွယ်ရေးအတွက် အရေးကြီးပါတယ်။ ပထမဦးစွာ၊ အလျားလိုက် ပိုလာရိုက်ဇ် အင်တင်နာဟာ ဒေါင်လိုက် ပိုလာရိုက်ဇ် အင်တင်နာနဲ့ ဆက်သွယ်မှာ မဟုတ်ပါဘူး။ အပြန်အလှန် သီအိုရမ်ကြောင့် အင်တင်နာဟာ ထုတ်လွှင့်ခြင်းနဲ့ လက်ခံခြင်းတွေကို တစ်ထပ်တည်း လုပ်ဆောင်ပါတယ်။ ဒါကြောင့် ဒေါင်လိုက် ပိုလာရိုက်ဇ် အင်တင်နာတွေဟာ ဒေါင်လိုက် ပိုလာရိုက်ဇ် စက်ကွင်းတွေကို ထုတ်လွှင့်ပြီး လက်ခံပါတယ်။ ဒါကြောင့် ဒေါင်လိုက် ပိုလာရိုက်ဇ် အလျားလိုက် ပိုလာရိုက်ဇ် အင်တင်နာကို ထုတ်လွှင့်ဖို့ ကြိုးစားရင် လက်ခံမှု ရရှိမှာ မဟုတ်ပါဘူး။
ယေဘုယျအားဖြင့်၊ ထောင့် ( ) ဖြင့် တစ်ခုနှင့်တစ်ခု လှည့်ပတ်နေသော linearly polarized antenna နှစ်ခုအတွက်၊ ဤ polarization mismatch ကြောင့်ဖြစ်ပေါ်လာသော power loss ကို polarization loss factor (PLF) ဖြင့် ဖော်ပြပါမည်။
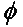
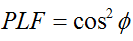
ထို့ကြောင့် အင်တင်နာနှစ်ခုတွင် polarization တူညီပါက ၎င်းတို့၏ ဖြာထွက်နေသော အီလက်ထရွန်စက်ကွင်းများကြားရှိ ထောင့်သည် သုညဖြစ်ပြီး polarization မကိုက်ညီမှုကြောင့် ပါဝါဆုံးရှုံးမှု မရှိပါ။ အင်တင်နာတစ်ခုသည် ဒေါင်လိုက် polarization ဖြစ်ပြီး အခြားတစ်ခုသည် အလျားလိုက် polarization ဖြစ်ပါက ထောင့်သည် ၉၀ ဒီဂရီဖြစ်ပြီး ပါဝါလွှဲပြောင်းပေးမည်မဟုတ်ပါ။
မှတ်ချက်- ဖုန်းကို ခေါင်းပေါ်မှ မတူညီသောထောင့်များသို့ ရွှေ့ခြင်းဖြင့် တစ်ခါတစ်ရံတွင် ရေဒီယိုလှိုင်းလက်ခံမှုကို တိုးမြှင့်နိုင်ရခြင်းအကြောင်းရင်းကို ရှင်းပြပါသည်။ ဆဲလ်ဖုန်းအင်တင်နာများသည် များသောအားဖြင့် လိုင်းယင့်ပိုလာရိုက်ဇ်ဖြစ်သောကြောင့် ဖုန်းကိုလှည့်ခြင်းဖြင့် ဖုန်း၏ပိုလာရိုက်ဇ်နှင့် ကိုက်ညီနိုင်ပြီး ရေဒီယိုလှိုင်းလက်ခံမှုကို တိုးတက်ကောင်းမွန်စေပါသည်။
စက်ဝိုင်းပုံ ပိုလာရိုက်ဇေးရှင်းသည် အင်တင်နာအများစု၏ လိုလားအပ်သော ဝိသေသလက္ခဏာတစ်ခုဖြစ်သည်။ အင်တင်နာနှစ်ခုစလုံးသည် စက်ဝိုင်းပုံ ပိုလာရိုက်ဇေးရှင်းဖြစ်ပြီး ပိုလာရိုက်ဇေးရှင်း မကိုက်ညီမှုကြောင့် အချက်ပြမှု ဆုံးရှုံးမှု မခံစားရပါ။ GPS စနစ်များတွင် အသုံးပြုသော အင်တင်နာများသည် ညာဘက်တွင် စက်ဝိုင်းပုံ ပိုလာရိုက်ဇေးရှင်း ရှိသည်။
ယခု linearly polarized antenna သည် circularly polarized waves များကို လက်ခံရရှိသည်ဟု ယူဆပါ။ အလားတူပင် circularly polarized antenna သည် linearly polarized waves များကို လက်ခံရရှိရန် ကြိုးစားသည်ဟု ယူဆပါ။ ရလဒ် polarization loss factor ကဘာလဲ။
circular polarization ဆိုတာ တကယ်တော့ orthogonal linearly polarized waves နှစ်ခုဖြစ်ပြီး phase ကနေ ၉၀ ဒီဂရီ လွဲနေတယ်ဆိုတာ သတိရပါ။ ဒါကြောင့် linearly polarized (LP) antenna ဟာ circularly polarized (CP) wave phase component ကိုသာ လက်ခံရရှိပါလိမ့်မယ်။ ဒါကြောင့် LP antenna မှာ polarization mismatch loss 0.5 (-3dB) ရှိပါလိမ့်မယ်။ LP antenna ဘယ်ထောင့်လှည့်လှည့် ဒါက မှန်ကန်ပါတယ်။ ဒါကြောင့်:
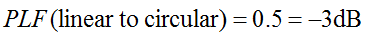
ပိုလာရိုက်ဇေးရှင်းဆုံးရှုံးမှုအချက်ကို တစ်ခါတစ်ရံတွင် ပိုလာရိုက်ဇေးရှင်းစွမ်းဆောင်ရည်၊ အင်တင်နာမကိုက်ညီမှုအချက် သို့မဟုတ် အင်တင်နာလက်ခံမှုအချက်ဟု ရည်ညွှန်းလေ့ရှိသည်။ ဤအမည်အားလုံးသည် သဘောတရားတစ်ခုတည်းကို ရည်ညွှန်းပါသည်။
ပို့စ်တင်ချိန်: ၂၀၂၃ ခုနှစ်၊ ဒီဇင်ဘာလ ၂၂ ရက်







